Games on Networks
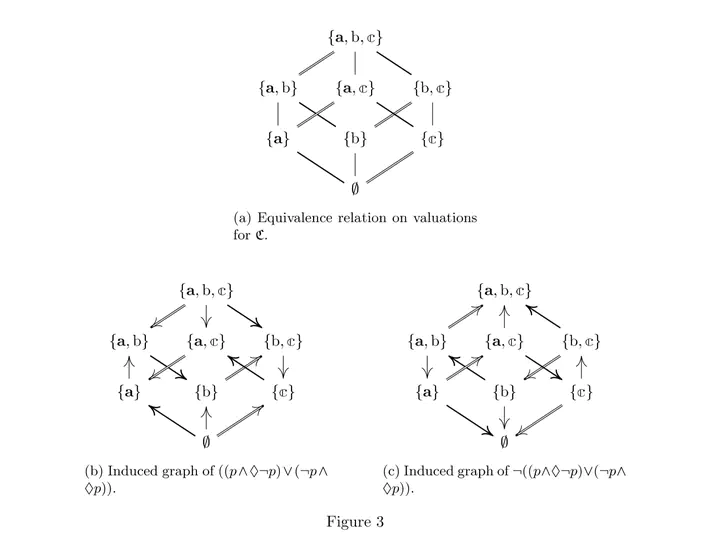Strategy profile graphs induced by goal structure in a network game.
Games played in social networks provide interesting models of numerous social phenomena. In a series of papers, I have investigated properties of Boolean Network Games and related models. A Boolean Network Game consists of a set of players arranged in a social network, each assigned a formula of modal logic as a goal to be made true. Each player has control over the valuation of propositions at their position in the network. The games are inter-reducible with Iterated Boolean Games, though with an exponential increase in size.
As a tool for studying games such as these, I have investigated Local Fact Change Logic, a model change modal logic with an operator which changes the valuation at the current world only. The addition of this simple operator causes satisfiability to become undecidable, and model-checking to leap to being PSPACE-complete.
